Reliability Analysis

Internal consistency reliability is typically estimated using a statistic called Cronbach’s alpha, which is the average correlation among all possible pairs of items, adjusting for the number of items. To estimate the Cronbach’s alpha of the BSS, go to the Analyze menu and select Factor→ Reliability Analysis.

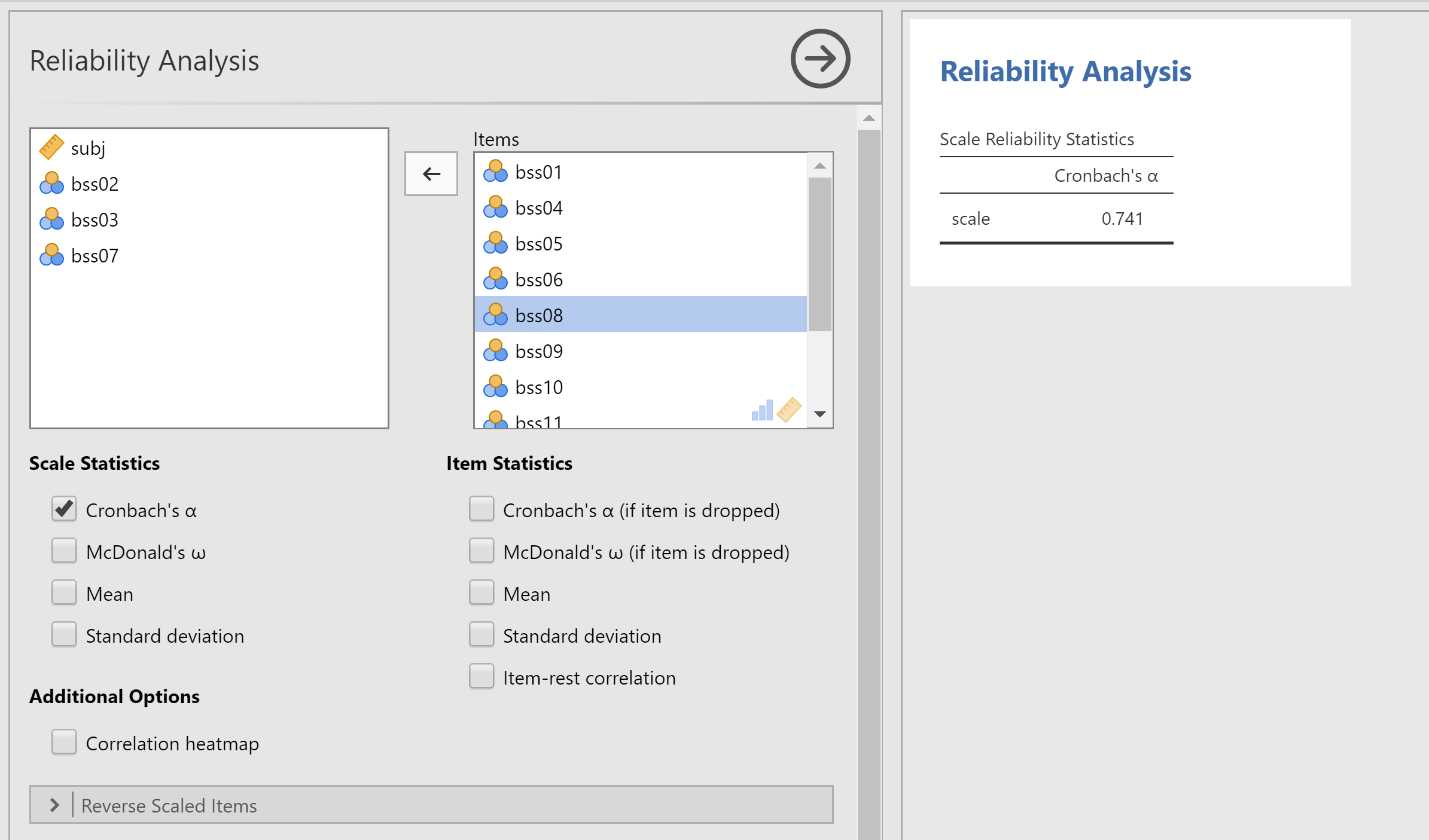
Select all the bss items and move them from the left window into the right window. Then, take back bss02, bss03, and bss07. You don’t want to include the original items bss02, bss03, and bss07 because they are phrased in the opposite direction of the other items.Type "BSS" as the "Scale label".

Jamovi is interactive. So any changes you make in the analysis on the left are instantsly shown in the results on the right.

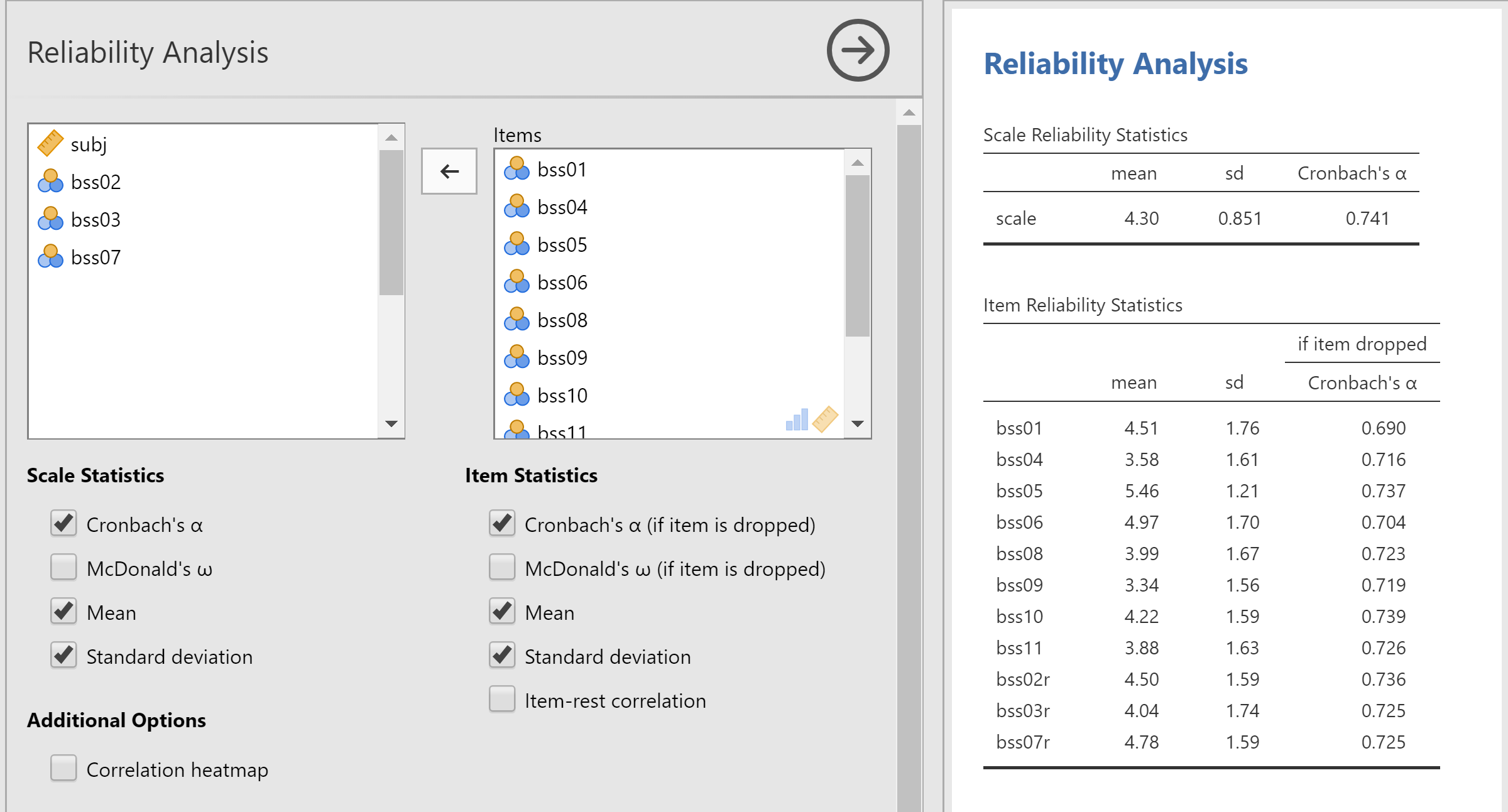
We need some statistics about our scale. So uncer the Scale Statitstics list on the left of the dialog, notics that "Chronbach's" is selected, and add "Mean" and "Standard Deviation" to the list of of selections. Under the Item Statistics lable below the list of items, select Chronbach's α (if item is dropped), Mean, and Standard Deviation.

Interpreting the Output

If all goes well, you will obtain output in the Output Window that begins with this:

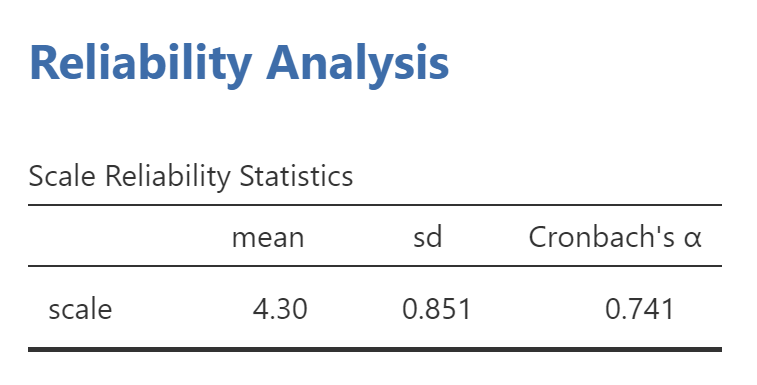
The output above tells you that the reliability analysis was able to use all 74 observations. If there are more than 10-15 percent of your observations that are excluded, you should check your data to make sure there isn’t a problem and also be cautious in generalizing your findings. The real meat of the analysis is presented at the end of the line.

This is Cronbach’s alpha, a measure of the internal consistency reliability of a set of measures. You will need to report the final Cronbach’s alpha of any multi-item measure you use. Remember that reliability is a number that ranges from 0 to 1, with values closer to 1 indicating higher reliability. Ideally, you want your measure to have a reliability above 0.7. Here, reliability is 0.741.

Next up are the item statistics:

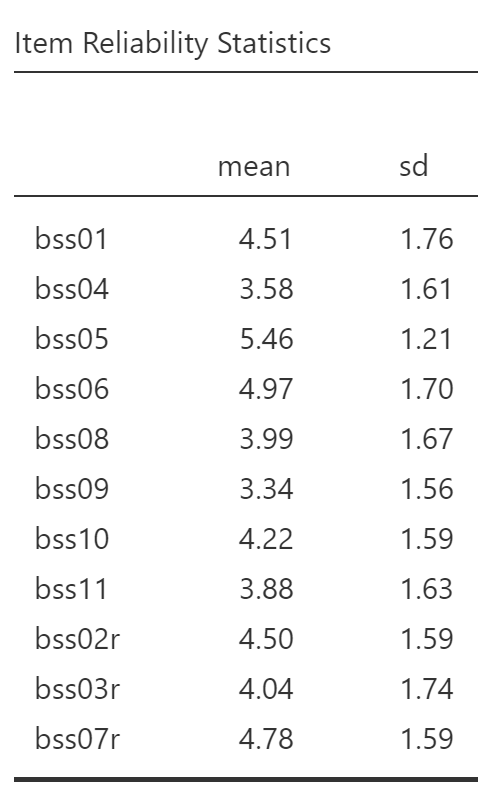
These tell you the mean and standard deviation for each variable. You might take note of any means that are especially high or low, as these suggest that many subjects either agreed or disagreed with the item. You would also want to verify that all the items are on a similar scale. That is, if the mean of one item is 4.51 and the mean of another item is 164.32, you should hesitate to simply average those two together because the second one would dominate. Finally, there are the item-total statistics, so called because they describe how each individual item relates to the total of all the items:

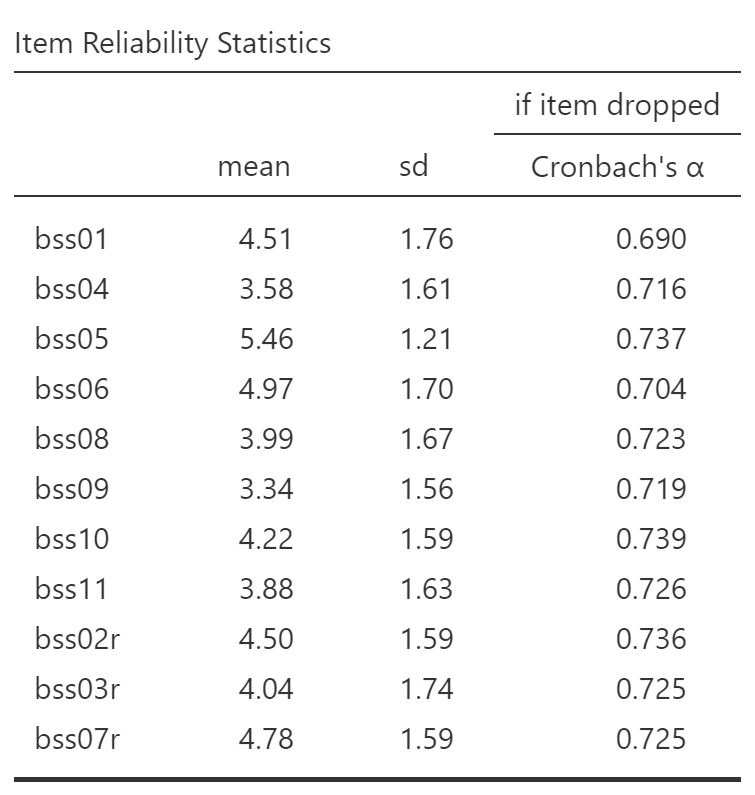
The last column in the above table is of most use to us. That column, titled "Item if Dropped Chronbach's α", tells you what Cronbach’s alpha would have been, had you gotten rid of just that one item. For example, if you had deleted (not included) bss01, Cronbach’s alpha would have decreased from 0.741 (which you got from the "Reliability Statistics" table above) to 0.690. Because higher reliabilities are better, deleting bss01 is a bad idea. In fact, all of the values in that column are less than 0.741, which means that you should not get rid of any of them.

Deleting Items to Improve Reliability

If you had found some variables whose Alpha if Item Deleted scores were higher than the scale’s alpha, then the next step would be to delete just one of them: the one with the highest alpha-if-item-deleted score. In the table above, which item has the highest alpha-if-item-deleted score? bss10. If we were going to improve this scale’s reliability and if bss10’s alpha-if-item-deleted score were greater than the overall alpha, then we would simply remove bss10 from the "Items" list and the analysis will rerun itself.

Be sure to delete items just one at a time, not all at once. The reason for this is that each time you delete one item, the effect on the other items can be hard to predict. Once you delete an item, do not put it back. After you delete an item and re-run the reliability analysis, look to see if any other items have alpha-if-item-deleted scores that are higher than the new overall alpha. If yes, continue to delete items and re-run the reliability analysis. If no, stop and keep the variables that remain.